Мадэляванне сістэм масавага абслугоўвання

1. Чэргі свабодных каналаў
2. спасылкі

Элементамі СМА з'яўляюцца:

• ўваходных (які ўваходзіць) струмень патрабаванняў (заявак) на абслугоўванне;
• прыборы (каналы) абслугоўвання;
• чаргу заявак, якія чакаюць абслугоўвання;
• выходны (які выходзіць) струмень обслуженных заявак;
• струмень не обслуженных заявак;
• чаргу свабодных каналаў (для шматканальных СМА).

Які ўваходзіць паток - гэта сукупнасць заявак на абслугоўванне. Часта заяўка атаясамліваецца з яе носьбітам. Напрыклад, паток няспраўнай радыёапаратуры, які паступае ў майстэрню аб'яднання, і ўяўляе сабой струмень заявак - патрабаванняў на абслугоўванне ў дадзенай СМА.

Як правіла, на практыцы маюць справу з так званымі рэкурэнтнага патокамі, патокамі, якія валодаюць ўласцівасцямі:

• стацыянарнага;
• ардынарных;
• абмежаванага паслядзеяння.

Першыя два ўласцівасці мы вызначылі раней. Што тычыцца абмежаванага паслядзеяння, то яно заключаецца ў тым, што інтэрвалы паміж паступаюць заяўкамі з'яўляюцца незалежнымі выпадковымі велічынямі.

Рэкурэнтнага патокаў шмат. Кожны закон размеркавання інтэрвалаў спараджае свой Рэкурэнтная струмень. Рэкурэнтнага патокі інакш называюць патокамі Пальма.

Менавіта такі паток мяркуюць праекціроўшчыкі пры распрацоўцы СМА. Выклікана гэта трыма прычынамі.

Па-першае, паток гэтага тыпу ў тэорыі масавага абслугоўвання аналагічны нармальнаму законе размеркавання ў тэорыі верагоднасцяў у тым сэнсе, што да найпростага патоку прыводзіць гранічны пераход для патоку, які з'яўляецца сумай патокаў з адвольнымі характарыстыкамі пры бясконцым павелічэнні складнікаў і памяншэнні іх інтэнсіўнасці. Гэта значыць сума адвольных незалежных (без перавагі) патокаў з інтэнсіўным з'яўляецца найпростым патокам з інтэнсіўнасцю

Па-другое, калі абслугоўваюць каналы (прыборы) разлічаныя на найпросты паток заявак, то абслугоўванне іншых тыпаў патокаў (з той жа інтэнсіўнасцю) будзе забяспечана з не меншай эфектыўнасцю.

Па-трэцяе, менавіта такі паток вызначае Маркоўскі працэс у сістэме і, такім чынам, прастату матэматычнага аналізу сістэмы. Пры іншых патоках аналіз функцыянавання СМА складзены.

Часта сустракаюцца сістэмы, у якіх паток ўваходных заявак залежыць ад колькасці заявак, якія знаходзяцца ў абслугоўванні. Такія СМА называюць замкнёнымі (інакш - растуленымі). Напрыклад, праца майстэрні сувязі аб'яднання можа быць прадстаўлена мадэллю замкнёнай СМА. Хай гэтая майстэрня прызначана для абслугоўвання радыёстанцый, якіх у аб'яднанні 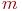. Кожная з іх мае інтэнсіўнасць адмоваў 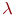. Ўваходны струмень адмовіла апаратуры будзе мець інтэнсіўнасць :

дзе - колькасць радыёстанцый, якiя ўжо знаходзяцца ў майстэрні на рамонце.

Заяўкі могуць мець розныя правы на пачатак абслугоўвання. У гэтым выпадку кажуць, што заяўкі неаднародныя. Перавагі адных патокаў заявак перад іншымі задаюцца шкалой прыярытэтаў.

Важнай характарыстыкай уваходнага патоку з'яўляецца каэфіцыент варыяцыі:

дзе 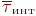- матэматычнае чаканне даўжыні інтэрвалу;

- сярэднеквадратычнае адхіленне выпадковай велічыні (даўжыні інтэрвалу) .

Для найпростага патоку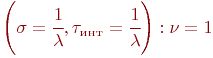

Для большасці рэальных патокаў .

пры паток рэгулярны, дэтэрмінаваных.

Каэфіцыент варыяцыі - характарыстыка, якая адлюстроўвае ступень нераўнамернасці паступлення заявак.

Каналы (прыборы) абслугоўвання. У СМА могуць быць адзін або некалькі абслугоўваюць прыбораў (каналаў). Згодна з гэтым СМА называюць аднаканальную або шматканальныя.

Шматканальныя СМА могуць складацца з аднатыпных або рознатыповых прыбораў. Абслуговымі прыборамі могуць быць:

• лініі сувязі;
• майстры рамонтных майстэрняў, прадаўцы, касіры;
• маршрутызатары ў кампутарных сетках;
• транспартныя сродкі;
• плацежныя тэрміналы;
• серверы, і інш.

Асноўная характарыстыка канала - час абслугоўвання. Як правіла, час абслугоўвання - велічыня выпадковая.

Звычайна практыкі мяркуюць, што час абслугоўвання мае экспанентны закон размеркавання:

дзе - інтэнсіўнасць абслугоўвання, ;

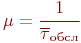- матэматычнае чаканне часу абслугоўвання.

Гэта значыць працэс абслугоўвання - Маркоўскі, а гэта, як цяпер нам вядома, дае істотныя выгоды ў колькасна-матэматычным мадэляванні.

Акрамя экспанентна сустракаюцца 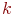-распределение Эрланген, гиперэкспоненциальное, трохкутнае і некаторыя іншыя. Гэта нас не павінна бянтэжыць, так як паказана, што значэнне крытэраў эфектыўнасці СМА мала залежаць ад выгляду закона размеркавання верагоднасцяў часу абслугоўвання.

Пры даследаванні СМА выпадае з разгляду сутнасць абслугоўвання, якасць абслугоўвання.

Каналы могуць быць абсалютна надзейнымі, гэта значыць не выходзіць з ладу. Дакладней, так можа быць прынята пры даследаванні. Каналы могуць валодаць канчатковай надзейнасцю. У гэтым выпадку мадэль СМА значна складаней.

Чарга заявак. У сілу выпадковага характару патокаў заявак і абслугоўвання якая прыйшла заяўка можа заспець канал (каналы) занятым абслугоўваннем папярэдняй заяўкі. У гэтым выпадку яна альбо пакіне СМА ня обслуженных, альбо застанецца ў сістэме, чакаючы пачатак свайго абслугоўвання. У адпаведнасці з гэтым адрозніваюць:

• СМА з адмовамі;
• СМА з чаканнем.

Даследчыка звычайна цікавяць такія статыстычныя характарыстыкі, звязаныя са знаходжаннем заявак у чарзе:

• сярэдняя колькасць заявак у чарзе за інтэрвал даследаванні;
• сярэдні час знаходжання (чакання) заяўкі ў чарзе. СМА з абмежаванай ёмістасцю чарзе адносяць да СМА змешанага тыпу.

СМА змешанага тыпу - такія СМА, у якіх заяўкі маюць абмежаваны час знаходжання ў чарзе незалежна ад яе ёмістасці.

Які выходзіць паток - гэта паток обслуженных заявак, якія пакідаюць СМА.

Сустракаюцца выпадкі, калі заяўкі праходзяць праз некалькі СМА: транзітная сувязь, вытворчы канвеер і т. П. У гэтым выпадку які выходзіць паток з'яўляецца уваходным для наступнай СМА.

Шматфазнай СМА, сеткі СМА - сукупнасць паслядоўна злучаных паміж сабой СМА

Які ўваходзіць паток першай СМА, прайшоўшы праз наступныя СМА, скажаецца і гэта абцяжарвае мадэляванне. Аднак, варта мець на ўвазе, што пры найпростым ўваходным струмені і экспанентны абслугоўванні (гэта значыць у Маркоўскіх сістэмах) выхадны паток таксама найпросты .Калі час абслугоўвання мае не экспанентнае размеркаванне, то які выходзіць струмень не толькі не найпросты, але і не Рэкурэнтная.

Заўважым, што інтэрвалы паміж заяўкамі які выходзіць патоку, гэта не тое ж самае, што інтэрвалы абслугоўвання. Бо можа апынуцца, што пасля заканчэння чарговага абслугоўвання СМА нейкі час прастойвае з-за адсутнасці заявак. У гэтым выпадку інтэрвал які выходзіць патоку складаецца з часу незанятасці СМА і інтэрвалу абслугоўвання першай, якая прыйшла пасля прастою, заяўкі.

У сістэмах з адмовамі ёсць паток необслуженных заявак. Калі ў СМА з адмовамі паступае Рэкурэнтная паток, а абслугоўванне - экспанентнае, то і струмень необслуженных заявак - Рэкурэнтная.

Чэргі свабодных каналаў

У шматканальных СМА могуць ўтварацца чэргі свабодных каналаў. Колькасць свабодных каналаў - велічыня выпадковая. Даследчыка могуць цікавіць розныя характарыстыкі гэтай выпадковай велічыні. Звычайна гэта сярэдні лік каналаў, занятых абслугоўваннем за інтэрвал даследаванні.

Такім чынам, па прыкметах, якія ўплываюць на функцыянаванне, СМА можа належаць да аднаго з тыпаў у адпаведнасці з прыведзенай класіфікацыяй (мал. 2.10).

класіфікацыя СМА

Для абазначэння простых (аднафазных) СМА выкарыстоўваецца сімволіка, прапанаваная Кендал:

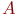- які ўваходзіць паток заявак: 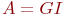- Рэкурэнтная паток; - найпросты струмень з паказальным законам размеркавання верагоднасцяў; - рэгулярны або дэтэрмінаваных паток (з пастаяннымі інтэрваламі паміж момантамі паступлення заявак).

- выпадковая працягласць абслугоўвання: або - рэкурэнтнага абслугоўванне з адной і той жа функцыяй размеркавання 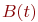для розных каналаў; 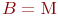- паказальнае абслугоўванне; - рэгулярнае абслугоўванне.

- колькасць абслугоўваюць каналаў. Калі n> 1, то сістэма называецца шматканальнай.

- колькасць месцаў для чакання заявак у чарзе. Калі , То СМА з стратамі (без чакання); - сістэма з неабмежаваным чаканнем; - сістэма з абмежаваным лікам месцаў для чакання.

спасылкі

Баёў В.Д., Сыпченко Р.П. камп'ютэрнае мадэляванне

Ці ведаеце Вы,

што "гравітацыйнае линзирование" нібыта назіранае паблізу далёкіх галактык (але не ў маштабе зорак, дзе яно павінна быць па формулах АМАіК!), На самай справе з'яўляецца тэрмічным линзированием , Звязаным са зменамі шчыльнасці эфіру ад нагрэву мірыядамі зорак. Больш падрабязна чытайце ў FAQ па эфірнай фізіцы .