Моделювання систем масового обслуговування

1. Черги вільних каналів
2. посилання

Елементами СМО є:

• вхідний (вхідний) потік вимог (заявок) на обслуговування;
• прилади (канали) обслуговування;
• чергу заявок, які очікують обслуговування;
• вихідний (вихідний) потік обслужених заявок;
• потік не обслужених заявок;
• чергу вільних каналів (для багатоканальних СМО).

Вхідний потік - це сукупність заявок на обслуговування. Часто заявка ототожнюється з її носієм. Наприклад, потік несправної радіоапаратури, що надходить в майстерню об'єднання, і являє собою потік заявок - вимог на обслуговування в даній СМО.

Як правило, на практиці мають справу з так званими рекурентними потоками, потоками, що володіють властивостями:

• стаціонарності;
• ординарности;
• обмеженого післядії.

Перші дві властивості ми визначили раніше. Що стосується обмеженого післядії, то воно полягає в тому, що інтервали між вступниками заявками є незалежними випадковими величинами.

Рекурентних потоків багато. Кожен закон розподілу інтервалів породжує свій рекурентний потік. Рекурентні потоки інакше називають потоками Пальма.

Саме такий потік припускають проектувальники при розробці СМО. Викликано це трьома причинами.

По-перше, потік цього типу в теорії масового обслуговування аналогічний нормальному закону розподілу в теорії ймовірностей в тому сенсі, що до найпростішого потоку призводить граничний перехід для потоку, що є сумою потоків з довільними характеристиками при нескінченному збільшенні доданків і зменшенні їх інтенсивності. Тобто сума довільних незалежних (без переваги) потоків з інтенсивностями є найпростішим потоком з інтенсивністю

По-друге, якщо обслуговуючі канали (прилади) розраховані на найпростіший потік заявок, то обслуговування інших типів потоків (з тією ж інтенсивністю) буде забезпечено з не меншою ефективністю.

По-третє, саме такий потік визначає марковский процес в системі і, отже, простоту математичного аналізу системи. При інших потоках аналіз функціонування СМО складний.

Часто зустрічаються системи, у яких потік вхідних заявок залежить від кількості заявок, що знаходяться в обслуговуванні. Такі СМО називають замкнутими (інакше - розімкнутими). Наприклад, робота майстерні зв'язку об'єднання може бути представлена ​​моделлю замкнутої СМО. Нехай ця майстерня призначена для обслуговування радіостанцій, яких в об'єднанні 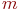. Кожна з них має інтенсивність відмов . Вхідний потік відмовила апаратури матиме інтенсивність :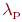

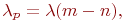
де - кількість радіостанцій, які вже перебувають в майстерні на ремонті.

Заявки можуть мати різні права на початок обслуговування. У цьому випадку говорять, що заявки неоднорідні. Переваги одних потоків заявок перед іншими задаються шкалою пріоритетів.

Важливою характеристикою вхідного потоку є коефіцієнт варіації:

де 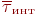- математичне очікування довжини інтервалу;

- середньоквадратичне відхилення випадкової величини (довжини інтервалу) .

Для найпростішого потоку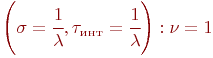

Для більшості реальних потоків .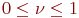

при потік регулярний, детермінований.

Коефіцієнт варіації - характеристика, яка відображає ступінь нерівномірності надходження заявок.

Вентиляційні канали (прилади) обслуговування. У СМО можуть бути один або декілька обслуговуючих приладів (каналів). Згідно з цим СМО називають одноканальними або багатоканальними.

Багатоканальні СМО можуть складатися з однотипних або різнотипних приладів. Обслуговуючими приладами можуть бути:

• лінії зв'язку;
• майстра ремонтних майстерень, продавці, касири;
• маршрутизатори в комп'ютерних мережах;
• транспортні засоби;
• платіжні термінали;
• сервери, і ін.

Основна характеристика каналу - час обслуговування. Як правило, час обслуговування - величина випадкова.

Зазвичай практики вважають, що час обслуговування має експонентний закон розподілу:

де 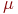- інтенсивність обслуговування, ;

- математичне очікування часу обслуговування.

Тобто процес обслуговування - марковский, а це, як тепер нам відомо, дає істотні зручності в чисельно-математичному моделюванні.

Крім експоненціального зустрічаються 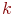-розподіл Ерланга, гиперекспониціональне трикутне і деякі інші. Це нас не повинно бентежити, оскільки показано, що значення критеріїв ефективності СМО мало залежать від виду закону розподілу ймовірностей часу обслуговування.

При дослідженні СМО випадає з розгляду сутність обслуговування, якість обслуговування.

Канали можуть бути абсолютно надійними, тобто не виходити з ладу. Вірніше, так може бути прийнято при дослідженні. Канали можуть мати кінцевої надійністю. У цьому випадку модель СМО значно складніше.

Черга заявок. В силу випадкового характеру потоків заявок і обслуговування прийшла заявка може застати канал (канали) зайнятим обслуговуванням попередньої заявки. В цьому випадку вона або покине СМО НЕ обслужених, або залишиться в системі, чекаючи початок свого обслуговування. Відповідно до цього розрізняють:

• СМО з відмовами;
• СМО з очікуванням.

Дослідника зазвичай цікавлять такі статистичні характеристики, пов'язані з перебуванням заявок в черзі:

• середня кількість заявок в черзі за інтервал дослідження;
• середній час перебування (очікування) заявки в черзі. СМО з обмеженою ємністю черзі відносять до СМО змішаного типу.

СМО змішаного типу - такі СМО, в яких заявки мають обмежений час перебування в черзі незалежно від її ємності.

Вихід двійкового - це потік обслужених заявок, які покидають СМО.

Зустрічаються випадки, коли заявки проходять через кілька СМО: транзитна зв'язок, виробничий конвеєр і т. П. У цьому випадку виходить потік є вхідним для наступного СМО.

Багатофазні СМО, мережі СМО - сукупність послідовно пов'язаних між собою СМО

Вхідний потік першої СМО, пройшовши через наступні СМО, спотворюється і це ускладнює моделювання. Однак, слід мати на увазі, що при простому вхідному потоці і експоненційному обслуговуванні (тобто в марковских системах) вихідний потік теж найпростіший .Якщо час обслуговування має не експоненціальне розподіл, то виходить потік не тільки не найпростіший, але і не рекурентний.

Зауважимо, що інтервали між заявками виходить потоку, це не те ж саме, що інтервали обслуговування. Адже може виявитися, що після закінчення чергового обслуговування СМО якийсь час простоює через відсутність заявок. У цьому випадку інтервал виходить потоку складається з часу незайнятості СМО і інтервалу обслуговування першої, яка прийшла після простою, заявки.

У системах з відмовами є потік необслужених заявок. Якщо в СМО з відмовами надходить рекурентний потік, а обслуговування - експоненціальне, то і потік необслужених заявок - рекурентний.

Черги вільних каналів

У багатоканальних СМО можуть утворюватися черги вільних каналів. Кількість вільних каналів - величина випадкова. Дослідника можуть цікавити різні характеристики цієї випадкової величини. Зазвичай це середнє число каналів, зайнятих обслуговуванням за інтервал дослідження.

Таким чином, за ознаками, що впливає на функціонування, СМО може належати до одного з типів відповідно до наведеної класифікацією (рис. 2.10).

Класифікація СМО

Для позначення простих (однофазних) СМО використовується символіка, запропонована Кендаллом:

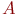- вхідний потік заявок: - рекурентний потік; - найпростіший потік з показовим законом розподілу ймовірностей; - регулярний або детермінований потік (з постійними інтервалами між моментами надходження заявок).

- випадкова тривалість обслуговування: або - рекуррентное обслуговування з однією і тією ж функцією розподілу для різних каналів; - показове обслуговування; - регулярне обслуговування.

- кількість обслуговуючих каналів. Якщо n> 1, то система називається багатоканальної.

- кількість місць для очікування заявок в черзі. якщо , То СМО з втратами (без очікування); - система з необмеженим очікуванням; 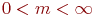- система з обмеженим числом місць для очікування.

посилання

Боїв В.Д., Сипченко Р.П. Комп'ютерне моделювання

Чи знаєте Ви,

що "гравітаційне лінзування" нібито спостерігається поблизу далеких галактик (але не в масштабі зірок, де воно повинно бути за формулами ОТО!), Насправді є термічним лінзуванням , Пов'язаним зі змінами щільності ефіру від нагрівання міріадами зірок. Детальніше читайте в FAQ по ефірної фізиці .